|
数缺形时少直观,形少数时难入微, |
|
|
|
|
构造法在高中数学中的应用 摘要 构造法解高中数学题,培养学生的思维能力。抓住问题的特征,联想熟知的数学模型,可以构造几何图形、构造函数及构造方程等,以便解决问题。基本的方法是:借用一类问题的性质,来研究另一类问题的思维方法。在解题过程中,若按习惯定势思维去探求解题途径比较困难时,可以启发学生根据题目特点,展开丰富的联想拓宽自己思维范围,运用构造法来解题也是培养学生创造意识和创新思维的手段之一,同时对提高学生的解题能力也有所帮助,用构造法解题,常使数学解题由难变易,它无一定之规,没有通用的构造法则。运用构造法解题对于培养思维的敏捷性和创造性,具有重要的意义。本文通过构造图形、构造方程、构造函数、构造模型等介绍了构造法在高中数学中的应用。构造法很重要。但由于它异于常规的思维,因此掌握起来有一定难度。只要不断在实践中摸索,去粗取精,相信会取得很好的效果。 关键词:构造法;创新;思维能力。 在解决某些数学问题时,我们常会采用这样的方法:通过对条件和结论充分细致的分析,抓住问题的特征,联想熟知的数学模型,然后变换命题,恰当地构造辅助元素,它可以是一个图形,一个函数,一个方程,一个等价命题等等,以此架起一座连接条件和结论的桥梁,从而使问题得以解决,这种解题的数学方法,我们称之为构造法。构造法是运用数学的基本思想经过认真的观察,深入的思考,构造出解题的数学模型从而使问题得以解决。构造法的内涵十分丰富,没有完全固定的模式可以套用,它是以广泛抽象的普遍性与现实问题的特殊性为基础,针对具体的问题的特点而采取相应的解决办法,其基本的方法是:借用一类问题的性质,来研究另一类问题的思维方法。在解题过程中,若按习惯定势思维去探求解题途径比较困难时,可以启发学生根据题目特点,展开丰富的联想拓宽自己思维范围,运用构造法来解题也是培养学生创造意识和创新思维的手段之一,同时对提高学生的解题能力也有所帮助,下面我们通过举例来说明通过构造法解题训练学生发散思维,谋求最佳的解题途径,达到思想的创新。历史上有不少著名的数学家,如欧几里得、欧拉、高斯、拉格朗日等人,都曾经用“构造法”成功地解决过数学上的难题。数学是一门创造性的艺术,蕴含着丰富的美,而灵活、巧妙的构造令人拍手叫绝,能为数学问题的解决增添色彩,更具研究和欣赏价值。近几年来,构造法及其应用又逐渐为数学教育界所重视,在数学竞赛中有着一定的地位。用构造法解题,常使数学解题由难变易,它无一定之规,没有通用的构造法则。运用构造法解题对于培养思维的敏捷性和创造性,具有重要的意义。下面通过几个实例说明构造法的应用。 一、构造图形 所谓有构造图形,是以已知为前提,构造一些理想的图形,其目的是通过这个图形直观地揭示已知与未来的关系,确定论证出发点,使证题的思路豁然开朗。华罗庚:“数离开形少直观,形离开数难入微。”利用数形结合的思想,可沟通代数,几何的关系,实现难题巧解。
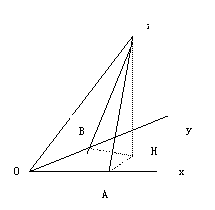
例1:设a,b,c是周长不超过2的三角形的三条边长, 求证:sina,sinb,sinc可以构成三角形的三条边长。 构造三面角 证明:由题意知道 a + b + c <2,且 a,b,c 是三角形三条边长,则a,b,c 可以 构成一个O-XYZ的三面角。 如图设a = ∠XOY,b = ∠XOZ,c =∠YOZ, 设OZ = 1,过Z作ZH垂直于面OXY,H为垂足, ∠HOZ=e,∠HOX=f,∠HOZ=g, 过H作HA⊥OX,HB⊥OY,A,B为垂足 Sin2b= AZ2 = AH2 + HZ2 = cos2e + cos2f +sin2z = sin2f + sin2ecos2f≥sin2f sinb≥sinf sinc≥sing 若两个式子都取“=”号,则f = g = 900,X,O,H共线与题设不符,若不能同时取等号 ,则sinb+sinc>sinf+sing≥sinfsing+cosfsing=sin(f+g)=sina 即sinb+sinc>sina,同理sina+sinb>sinc,sina+ sinc>sinb 所以sina,sinb,sinc可以构成三角形的三条边长 例2: 设x,y是正实数,求证:++≥ 构造一个三棱锥,让∠AVB = ∠BVC = ∠CVA =300
设VA=x, VC=y,VB= 则AB=,BC=,AC= 沿VB把三棱锥展开得:AB + AC + ,C≥B,= = 所以++≥
例3 若α、β、γ均为锐角,且满足cos2α+cos2β+cos2γ=1,求证:tanα·tanβ·tanγ≥2. 导析:拿到此题,联想到长方体对角线与三条棱所成角的性质,可构造长方体.设三度长分别为a、b、c,且交于顶点B的三棱与对角线BD1的夹角分别为α、β、γ.于是,原有三角不等式转化为代数不等式,即 tanα·tanβ·tanγ≥2. 二.构造方程 方程是解数学题的一个重要工具,许多数学问题,根据其数量关系,在已知和未知之间搭上桥梁,有目的构造方程,以沟通问题中条件与结论的联系,使问题中的隐含关系明朗化,从而简捷迅速地使问题获解,这是解某些竞赛题的常用技巧之一. 例4:若(z-x)2-4(x-y)(y-z)=0 求证:x、y、z成等差数列。 分析:本题证明方法很多,可以用构造法证明。注意到条件中的等式右边代数式的结构特点,容易联想起一元二次方程根的判别式,为此可构造以(z-x)2-4(x-y)(y-z)为判别式的一元二次方程(x-y)t2+(z-x)t+(y-z)=0 ( * ) 由题可知⊿ =(z-x)2-4(x-y)(y-z)=0 ∴方程(*)有两个相等实根 又∵(x-y)+(z-x)+(y-z)=0 ∴t=1为方程(*)的一个根,从而t1=t2=1 由韦达定理得:t1·t2= 从而2y=x+z,命题得证。 例5:上一个有10级的台阶,每步可上一级或两级,共有多少种上台阶的方法? 解析:设x表示上一级台阶的步数,表示上两级台阶的步数,则x + 2y=10(x≥0,y≥0,x,y∈Z) 当x=2,y=4时,6步走完10级台阶的方法为种; 当x=0,4,6,8,10,对应的y的取值分别为5,3,2,1,0,相应的上台阶的方法为,,,和。 故总的上台阶的方法为:+++++=89。 注:构造方程的关键是:找到等量关系,正确列出方程。 三、构造函数 函数在我们整个中学数学是占有相当的内容,学生对于函数的性质也比较熟悉。选择烂熟于胸的内容来解决棘手问题,同时也达到了训练学生的思维,增强学生的思维的灵活性,开拓性和创造性。 例6:已知a, b, m∈R+,且a < b 求证: <(高中数学苏教版选修2-2) 分析:由 已知,若用x 代替m呢?可以得到 是关于x 的分式,若我们令 是一个函数,且x ∈R+联想到这时,我们可以构造函数f(x)= 而又可以化为1+ 而我们又知道 在[0,∞] 内是增函数,从而便可求解。 证明:构造函数f(x)= 在[0,∞] 内是增函数, 即得
有些数学题似乎与函数毫不相干,但是根据题目的特点,巧妙地构造一个函数,利用函数的性质得到了简捷的证明。解题过程中不断挖掘学生的潜在意识而不让学生的思维使注意到某一点上,把自己的解题思路搁浅了。启发学生思维多变,从而达到培养学生发散思维。 四、构造模型 构造模型常用于隔板模型、抽屉原则及染色问题,也是各级数学竞赛中常用的方法,下面分别举例介绍构造模型。 例7:某中学准备组建一个18人的足球队,这18人由高一年级10个班的学生组成,每个班级至少一人,名额分配的方案共有多少种? 解析:运用隔板法必须同时具备三个条件:①所有元素必须相同;②所有元素必须分完;③没组至少有一个元素。本题符合要求,构造一个隔板模型,即把排成一行的18个人分成10组的方法数,这样用9块闸板插在17个间隔中,共有=24310种。即原问题有24310种不同分法。 例8:有17位科学家,其中每一人和其他所有人通信,他们通信中只讨论三个题目,且每两个科学家之间只讨论一个问题。 求证:至少有三个科学家之间讨论同一题目。 证明:构造模型 将原题转化为:空间17个点两两连线,用红、蓝、白三色染其边,每边一色。 求证:必存在同色三角形。 考虑由A点引出的16条线段颜色,至少6条同色。不妨设其同红,另一端点分别为A2、A3……A7,再考虑这6个点两两连线的颜色 1.有一条为红色,则存在红色三角形 2.无红色,则6色只能是蓝、白色,不妨考虑由A2点引出的5条线段颜色,至少有在同色,不妨设与A3、A4、A5连线同色。 (A)A3、A4、A5中任一条与它们同色,则存在同色三角形 ( B) A3、A4、A5中任一条不与它们同色,则三角形A3A4A5同色,存在同色三角形。 综合1.2.必存在同色三角形。 命题证毕。 注:根据问题的特点,把握问题的本质,联想、类比是构造模型的关键。 由此可见,构造法是多么重要。但由于它异于常规的思维,因此掌握起来有一定难度。只要不断在实践中摸索,去粗取精,相信会取得很好的效果。
参考文献: [1]、郑毓信:数学方法论; [2]、宋玉连:构造法在解题中的应用刍议; [3]、王国军:证明不等式的常用处理技巧; [4]、丘瑞立:中学数学方法论; [5]、叶文明:构造法解数学题。
|
|