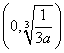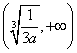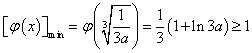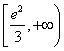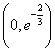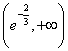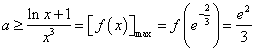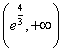2012届江苏省南京市高三三模第14题的解

-
2012届苏锡常镇四市高三第二次调研
第14题的解
14.设实数
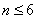 ,若不等式
,若不等式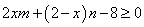 对任意
对任意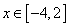 都成立,则
都成立,则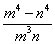 的最小值为
▲
.
的最小值为
▲
.解法1:不等式即
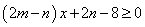 ,考虑函数
,考虑函数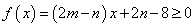 对任意
对任意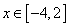 都成立,则
都成立,则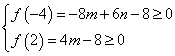 ,所以
,所以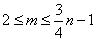 ,
,考虑
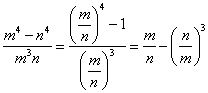 ,而函数
,而函数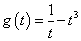 在
在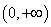 内是单调减函数,
内是单调减函数,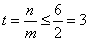 ,所以
,所以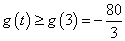 ,故
,故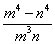 的最小值为
的最小值为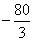 .
.
2012届江苏省宿迁、徐州市高三三模
第14题的解
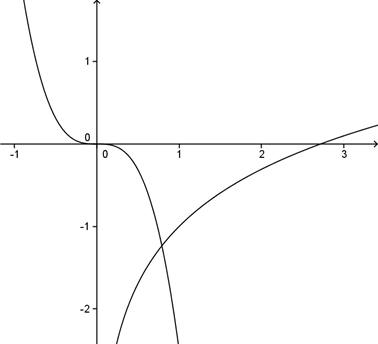
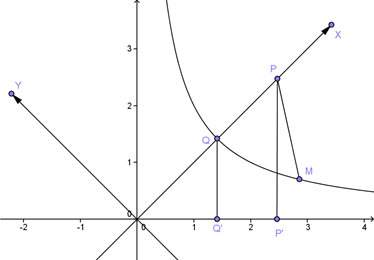
14.已知直线![]() 与函数
与函数![]() 的图象交于点
的图象交于点![]() ,
,![]() 、
、![]() 分别是直线
分别是直线![]() 与函数
与函数![]() 的图象上异于点
的图象上异于点![]() 的两点.若对于任意点
的两点.若对于任意点![]() ,
,![]() 恒成立,则点
恒成立,则点![]() 横坐标的取值范围是
▲
.
横坐标的取值范围是
▲
.
解法1:易得![]() ,设
,设![]() ,
,![]() ,由
,由![]() 恒成立可知,
恒成立可知,![]() ,即
,即![]() ,
,
整理得,![]() ,
,![]() ,
,
考虑函数![]() 对应方程的
对应方程的![]() 恒成立,所以
恒成立,所以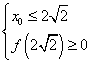 ,解得
,解得![]() ,故点
,故点![]() 横坐标的取值范围是
横坐标的取值范围是![]() .
.
解法2:易得![]() ,设
,设![]() ,
,![]() ,由
,由![]() 恒成立可知,
恒成立可知,![]() ,即
,即![]() ,
,
整理得,![]() ,
,![]() ,
,
考虑函数![]() 对任意的
对任意的![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立,而
恒成立,而![]() ,所以
,所以![]() ,故点
,故点![]() 横坐标的取值范围是
横坐标的取值范围是![]() .
.
同事罗冬丰老师的想法:
解法3:考虑标准形式的双曲线,![]() ,设
,设![]() ,
,![]() ,其中
,其中![]() ,则
,则![]() ,即
,即![]() ,整理得,
,整理得,![]() ,
,![]() ,即原坐标系下的
,即原坐标系下的![]() .故点
.故点![]() 横坐标的取值范围是
横坐标的取值范围是![]() .
.
2012届江苏省南通市高三三模第14题的解
第14题
法一:令OD=x,OE=y,由余弦定理得DE2=x2+y2+xy,CD2=x2+1-x.
CE2=y2+1-y,再由![]() 得2x2+2y2+xy
-x-y+2=
得2x2+2y2+xy
-x-y+2=![]() .即2(x+y)2-3xy
-x-y=
.即2(x+y)2-3xy
-x-y=![]()
因为xy≤![]() ,所以2(x+y)2-3
,所以2(x+y)2-3![]() -x-y≤
-x-y≤![]() ,整理得45(x+y)2-36(x+y)-32≤0
,整理得45(x+y)2-36(x+y)-32≤0
解之得:![]() ≤x+y≤
≤x+y≤![]() .
.
法二:同一得2(x+y)2-3xy
-x-y=![]() ,令t=x+y,y=t-x,代入得27x2-27tx+18t2-9t-8=0.①
,令t=x+y,y=t-x,代入得27x2-27tx+18t2-9t-8=0.①
则t的取值范围等价于方程①在(0,1)上有2个不同的解
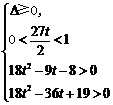 解之得:
解之得:![]() .
.
本题原是求x+y的取值范围的,用法一也可得出x+y的取值范围.

2012届江苏省南通市高三三模第13题的解
-
13.若函数
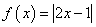 ,则函数
,则函数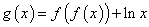 在
在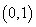 上不同零点的个数为 ▲ .
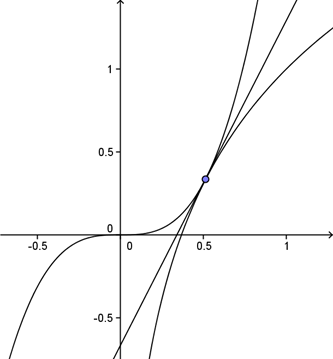
上不同零点的个数为 ▲ .解法1:考虑函数
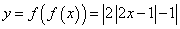 与
与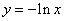 的图象交点,
的图象交点,而函数
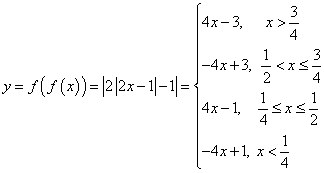 ,作图,
,作图,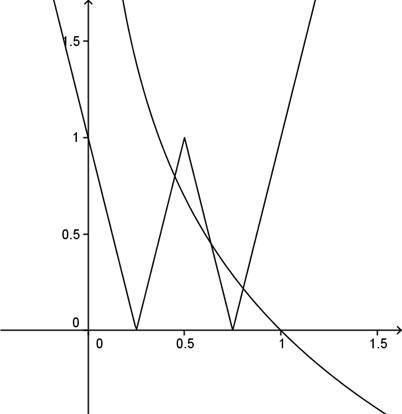
易见结果为3.
2012届苏北四市(徐州、淮安、连云港、宿迁)高三第二次质量检测第14题的解
14.已知![]() 的三边长
的三边长![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,则实数
,则实数![]() 的取值范围是
.
的取值范围是
.
解法1:由题意知,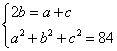 ,消去
,消去![]() 得,
得,![]() ,解得
,解得![]() ,
,
又设公差为![]() ,则
,则![]() ,所以
,所以![]() ,则
,则![]() ,解得
,解得![]() ,故
,故![]() .
.
解法2:(法1的优化——基本量)设公差为![]() ,则
,则![]() ,所以
,所以![]() ,则
,则![]() ,所以
,所以![]() ,解得
,解得![]() .
.
解法3:不妨设![]() ,由
,由![]() 可知,
可知,![]() ,
,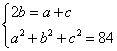 ,消去
,消去![]() 得,
得,![]() ,关于
,关于![]() 的二次方程
的二次方程![]() 在
在![]() 内存在实根,即
内存在实根,即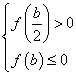 ,解得
,解得![]() .
.
2012届苏北四市(徐州、淮安、连云港、宿迁)高三第二次质量检测第13题的解
13.在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,
,![]() ,则当
,则当![]() 四边形的周长最小时,过三点
四边形的周长最小时,过三点![]() ,
,![]() ,
,![]() 的圆的圆心坐标是
.
的圆的圆心坐标是
.
解法1:由题意知,所求即要确定![]() 的最小值,考虑它表示动点
的最小值,考虑它表示动点![]() 与两定点
与两定点![]() 、
、![]() 的距离和,易得当
的距离和,易得当![]() 时,和为最小,此时可求得圆心坐标为
时,和为最小,此时可求得圆心坐标为![]() .
.
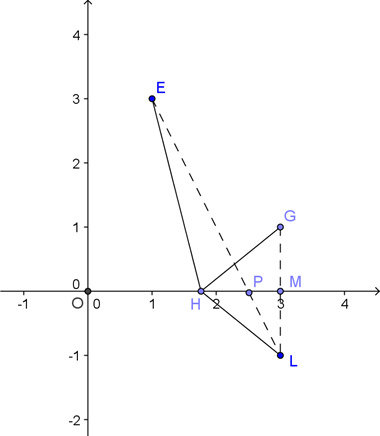
解法2:取点![]() ,则四边形
,则四边形![]() 为平行四边形,所求即
为平行四边形,所求即![]() 的最小,易得当三点
的最小,易得当三点![]() 、
、![]() 、
、![]() 共线时,即
共线时,即![]() ,求得圆心坐标为
,求得圆心坐标为![]() .
.
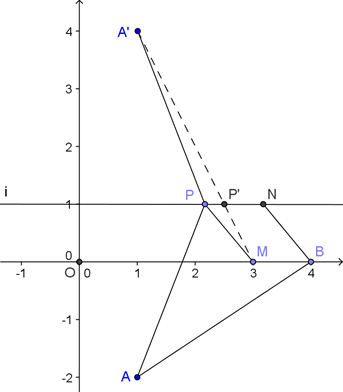
2012届苏中三市(南通、扬州、泰州)高三第一次调研测试第14题的解
14.各项均为正偶数的数列![]() 中,前三项依次成公差为
中,前三项依次成公差为![]() 的等差数列,后三项依次成公比为
的等差数列,后三项依次成公比为![]() 的等比数列,若
的等比数列,若![]() ,则
,则![]() 的所有可能的值构成的集合为
.
的所有可能的值构成的集合为
.
解法1:设公差为![]() ,则各数为
,则各数为![]() ,
,![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() ,则
,则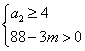 ,解得
,解得![]() .
.
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,此时数列为
,此时数列为![]() ,
,![]() ,
,![]() ,
,![]() ,不符合题意;
,不符合题意;
![]() 时,
时,![]() ,此时数列为
,此时数列为![]() ,
,![]() ,
,![]() ,
,![]() ,公比
,公比![]() ;
;
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,此时数列为
,此时数列为![]() ,
,![]() ,
,![]() ,
,![]() ,公比
,公比![]() .
.
综上,![]() 的所有可能的值构成的集合为
的所有可能的值构成的集合为![]() .
.
2012届盐城市高三第二次质量检测第14题的解(徐州一中的张培强老师解答)
14.在等差数列![]() 中,
中,![]() ,
,![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 对恒成立,则正整数
对恒成立,则正整数![]() 的最小值为
的最小值为
.
解法1:易得![]() ,则
,则![]() ,
,
考虑![]()
![]() ,
,
所以![]() ,则
,则![]() ,故所求为5.
,故所求为5.
-
2012届镇江市高三第一次模考第14题的解答
14.设不等式
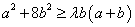 对任意
对任意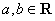 恒成立,则
恒成立,则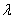 的取值范围为
▲ .
的取值范围为
▲ .解法1:(1)若
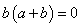 ,则不等式恒成立;
,则不等式恒成立;(2)若
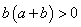 ,则
,则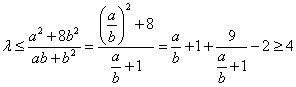 ,此时
,此时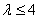 ;
;(2)若
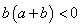 ,则
,则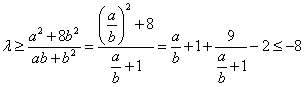 ,此时
,此时 ;
;综上所述,
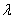 的取值范围为
的取值范围为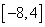 .
.解法2:原不等式即,
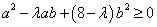 ,
,若
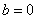 则不等式恒成立,
则不等式恒成立,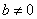 时,即有
时,即有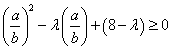 ,则
,则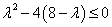 ,解得
,解得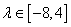 .
.2012届江苏省无锡市高三期末调研第13题的解答
13.设点
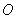 是
是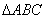 的三边中垂线的交点,且
的三边中垂线的交点,且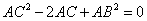 ,则
,则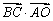 的范围是 .
的范围是 .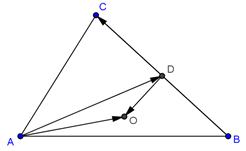
解法1:设
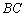 边上的中垂线的垂足为
边上的中垂线的垂足为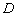 ,
,则
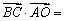
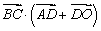
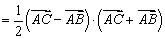
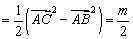 ,
,考虑
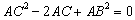 变形为
变形为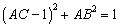 ,易得
,易得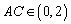 ,
,联立
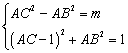 ,消去
,消去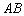 可得,
可得,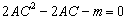 ,其有
,其有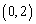 内的根,
内的根,易求得
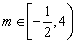 ,故
,故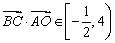 .
.解法2:设
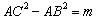 ,考虑几何意义,双曲线
,考虑几何意义,双曲线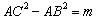 与圆
与圆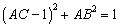 有位于
有位于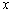 轴上方的公共点.
轴上方的公共点.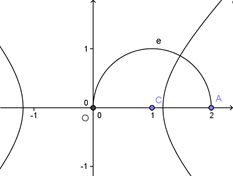
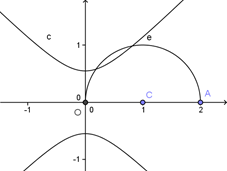
易得
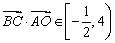 .
.2012届江苏省高三样本分析调研第14题的解答
14.已知定义域为
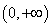 的单调函数
的单调函数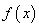 ,若对任意的
,若对任意的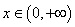 都
都有
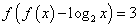 ,则满足方程
,则满足方程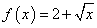 的所有根的和为___________.
的所有根的和为___________.解法:由
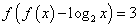 恒成立可知,
恒成立可知,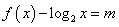 (
(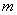 为一常数),
为一常数),而
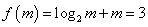 ,所以
,所以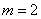 ,即有
,即有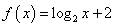 ,
,则方程
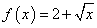 即
即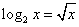 .易得其根为4和16,结果为20.
.易得其根为4和16,结果为20.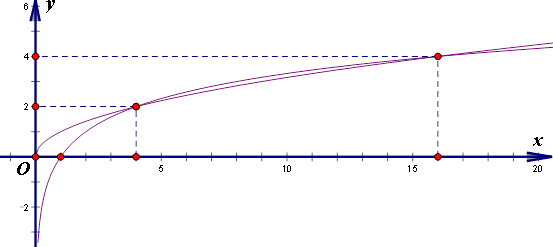
2012届江苏省常州市高三期末调研第12题的解答
12.已知
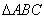 中,
中,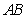 边上的高与
边上的高与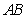 边的长相等,则
边的长相等,则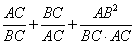 的最大值为___________.
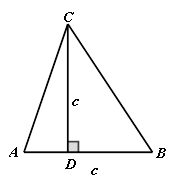
的最大值为___________.解法:(巫老师提供)设
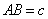 ,
,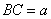 ,
,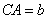 ,则
,则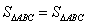 ,即
,即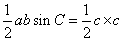 ,所以
,所以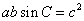 ,
,则
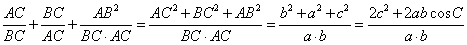
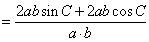
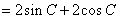
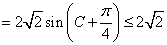 ,当
,当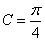 时,所求最大值为
时,所求最大值为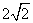 .
.
原型题:
设
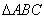 的
的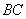 边上的高
边上的高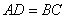 ,
,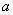 ,
,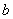 ,
,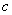 分别表示角
分别表示角 ,
,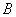 ,
,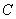 对应的三边,则
对应的三边,则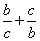 的取值范围是___________.
的取值范围是___________.解析:由题意知,
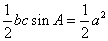 ,所以
,所以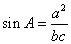 ,由余弦定理有,
,由余弦定理有,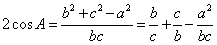 ,所以
,所以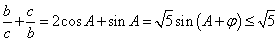 ,又
,又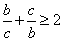 ,故
,故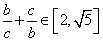 .
.2012届江苏省常州市高三期末调研第13题的解答
13.已知函数
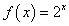 ,且
,且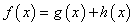 ,其中
,其中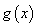 为奇函数,
为奇函数,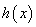 为偶函数,若不等式
为偶函数,若不等式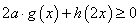 对任意
对任意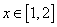 恒成立,则实数
恒成立,则实数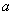 的取值范围为___________.
的取值范围为___________.解法:由题意知,
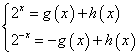 ,所以
,所以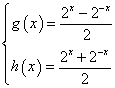 ,不等式
,不等式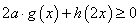 即
即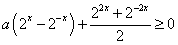 ,即
,即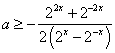 ,令
,令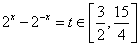 ,则
,则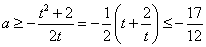 ,故实数
,故实数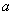 的取值范围为
的取值范围为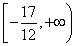 .
.2012届江苏省常州市高三期末调研第14题的解答
14.已知
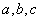 均为正实数,记
均为正实数,记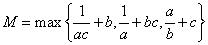 ,则
,则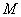 的最小值为 ▲ .
的最小值为 ▲ .解法1:由题意知,
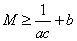 ,
,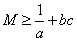 ,
,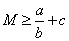 ,所以
,所以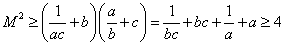 ,当且仅当
,当且仅当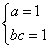 时,取等;
时,取等;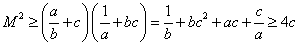 ,当且仅当
,当且仅当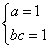 时,取等;
时,取等;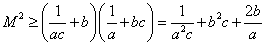 ,
,特别地,当
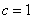 时,
时,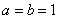 ,
,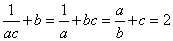 ,有
,有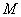 的最小值为2.
的最小值为2.解法2:

2012届江苏省南通市高三期末调研第14题的解答
14、函数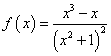 的值域是
.
的值域是
.
解析1:易知![]() 为奇函数,故只需求
为奇函数,故只需求![]() 内的值域,
内的值域,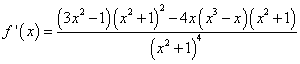
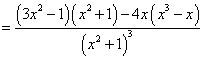
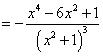 ,令
,令![]() ,解得
,解得![]() ,所以
,所以![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
↘ |
|
↗ |
|
↘ |
故值域为
解析2: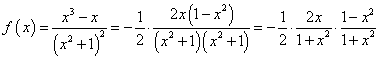 ,令
,令![]() ,则
,则![]() .
.
解析3: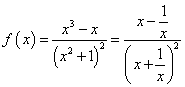 ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,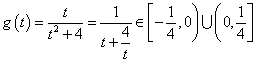 ,故值域为
,故值域为
2012届江苏省南通市高三期末调研第13题的解答
13、设![]() 是双曲线
是双曲线![]() 的右焦点,双曲线两渐近线分别为
的右焦点,双曲线两渐近线分别为![]() 、
、![]() ,过
,过![]() 作直线
作直线![]() 的垂线,分别交
的垂线,分别交![]() 、
、![]() 于两点,若
于两点,若![]() 、
、![]() 、
、![]() 成等差数列,且向量
成等差数列,且向量![]() 与
与![]() 同向,则双曲线的离心率
同向,则双曲线的离心率![]() 的大小为
.
的大小为
.
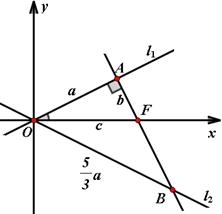 解析1:如图,由题意知,
解析1:如图,由题意知,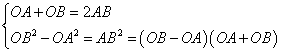 ,即
,即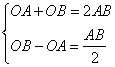 ,所以
,所以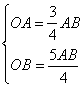 ,则
,则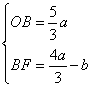 ,由角平分线定理可得,
,由角平分线定理可得,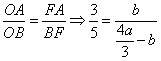 ,所以
,所以![]() ,则易得
,则易得![]() .
.
解析2:如图,由题意知,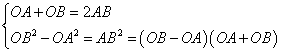 ,即
,即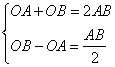 ,所以
,所以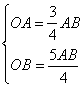 ,则
,则![]() ,由
,由![]() 可得,
可得,![]() ,解得
,解得![]() .
.
解析3:由题意知,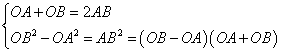 ,即
,即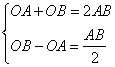 ,所以
,所以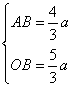 ,则
,则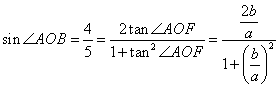 ,解得
,解得![]() ,则
,则![]() .
.
2012届苏州市高三第一次调研第14题的解答
14.设![]() 均为大于1的自然数,函数
均为大于1的自然数,函数![]() ,
,![]() ,若存在实数
,若存在实数![]() ,使得
,使得![]() ,则
,则![]() ▲ .
▲ .
解法1:存在![]() 使得
使得![]() 即存在
即存在![]() 使得
使得![]() ,则
,则![]()
![]()
![]() ,所以
,所以![]() ,即
,即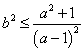
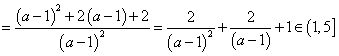 ,可得
,可得![]() ,故
,故![]()
2012届南京市、盐城市高三第一次模考第14题的解答
14.设![]() ,
,![]() ,
,![]() ,若对任意的正实数
,若对任意的正实数![]() ,都存在以
,都存在以![]() 为三边长的三角形,
为三边长的三角形,
则实数![]() 的取值范围是
▲ .
的取值范围是
▲ .
解法1:由题意知,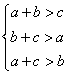 恒成立,即
恒成立,即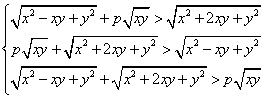 ,
,
即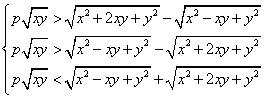 ,即
,即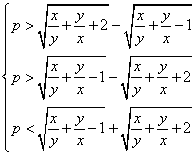 ,解得
,解得![]() .
.
解法2:显然![]() ,故只需考虑
,故只需考虑![]() ,
,
即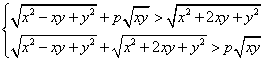 ,即
,即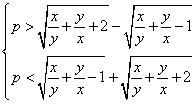 ,解得
,解得![]() .
.
解法3: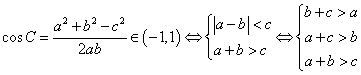 ,
,
(江苏省涟水中学
谈玉楼老师解法)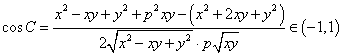 ,
,
即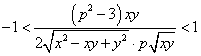 ,
,
即![]() ,
,
即![]() ,
,
即![]() ,即
,即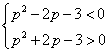 ,即
,即 ,故
,故![]() .
.
(感谢徐州一中的张培强老师解答)